In de rijke geschiedenis van de wiskunde heeft de Stelling van Pythagoras een bijzondere plaats ingenomen. Deze stelling, vernoemd naar de oude Griekse wiskundige Pythagoras, is een fundamenteel concept in de meetkunde, dat tot op de dag van vandaag relevant is. Het is belangrijk op te merken dat veel details over het leven van Pythagoras omgeven zijn door legendes en mythen en het kan moeilijk zijn om exacte historische informatie over hem te vinden. Desondanks heeft zijn invloed op de wiskunde en de ontwikkeling van het wiskundig denken een blijvende indruk achtergelaten..
Pythagoras
Pythagoras werd rond 570 voor Christus geboren op het eiland Samos en reisde naar verschillende plaatsen, waaronder Egypte, voordat hij zich in Croton, een Griekse kolonie in Zuid-Italië, vestigde. Daar richtte hij een school op waar zijn ideeën werden onderwezen en verspreid. Hij was niet alleen een wiskundige, maar ook een filosoof en mysticus. Hij richtte de beroemde Pythagoreïsche school op, waar zijn volgelingen zich bezighielden met diverse wetenschappelijke en filosofische onderwerpen. Ondanks de impact die Pythagoras had, is het belangrijk te benadrukken dat veel van zijn biografische gegevens zijn gehuld in mysterie en legendes. Hierdoor is het soms moeilijk om onderscheid te maken tussen historische feiten en mythische elementen in zijn verhaal.
Pythagoreïsme
Naast zijn bijdragen aan de geometrie had Pythagoras ook invloed op de filosofie en religie. Hij stichtte een religieuze beweging die bekend staat als het Pythagoreïsme. Deze beweging combineerde wiskundige studies met mystieke en spirituele overtuigingen. Pythagoras en zijn volgelingen geloofden dat getallen fundamentele eigenschappen van het universum vertegenwoordigen en een diepere betekenis hebben.
Pythagoreïsche Stelling
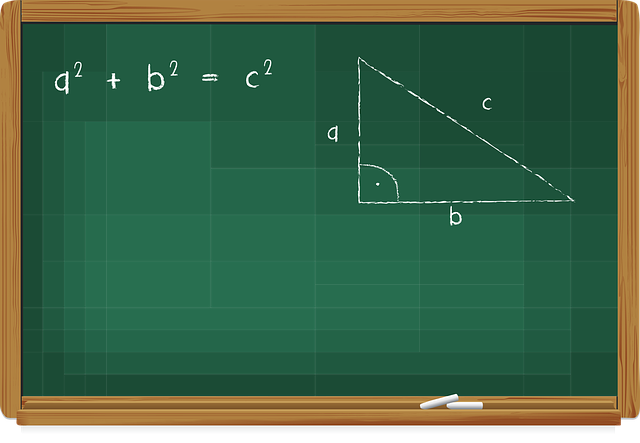
De stelling van Pythagoras, die zegt dat in een rechthoekige driehoek de som van de kwadraten van de rechthoekszijden gelijk is aan het kwadraat van de schuine zijde, heeft brede toepassingen in de wiskunde en natuurwetenschappen. Het vormt de basis voor de studie van driehoeksmeetkunde en heeft invloed gehad op diverse wetenschappelijke disciplines.
De stelling die zijn naam draagt, werd echter niet rechtstreeks aan hem toegeschreven. Het was eerder een ontwikkeling binnen de Pythagoreïsche school. De stelling luidt als volgt: in een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa gelijk aan de som van de kwadraten van de lengten van de twee andere zijden. In wiskundige termen is dit als volgt uitgedrukt: a2 + b2 = c2.
Bewijs en Verfijningen
Het bewijs van de Pythagoreïsche Stelling heeft door de eeuwen heen verschillende vormen aangenomen. Een van de oudste en meest bekende bewijzen is het geometrische bewijs, waarbij vier kopieën van de rechthoekige driehoek worden gebruikt om een vierkant te vormen. Elk van deze driehoeken bevindt zich aan een zijde van het vierkant, en het is duidelijk dat het vierkant opgebouwd uit deze driehoeken gelijk is aan het vierkant opgebouwd uit de zijden van de driehoek.
Naast het klassieke bewijs zijn er door de eeuwen heen verschillende alternatieve bewijzen ontwikkeld, waaronder algebraïsche en zelfs niet-wiskundige benaderingen.
Toepassingen in de Wereld
De Pythagoreïsche Stelling is niet alleen een abstract wiskundig concept, maar heeft ook tal van praktische toepassingen in verschillende disciplines. In de architectuur wordt de stelling bijvoorbeeld gebruikt om de lengte van diagonale lijnen in rechthoekige gebouwen te berekenen. In de natuurkunde wordt het toegepast bij het oplossen van problemen met betrekking tot afstanden, snelheden en krachten.
Daarnaast heeft de stelling toepassingen in de informatica, beeldverwerking en zelfs in de muziektheorie. Het is opmerkelijk hoe een ontdekking uit het oude Griekenland zijn stempel heeft gedrukt op zo’n breed scala aan wetenschappelijke en praktische gebieden.
Conclusie
De Pythagoreïsche Stelling blijft een van de meest essentiële en invloedrijke concepten in de geschiedenis van de wiskunde. Haar eenvoudige maar krachtige verklaring heeft de deur geopend naar een dieper begrip van de meetkunde en heeft geleid tot talloze toepassingen in diverse disciplines. Als eerbetoon aan de oude Griekse geleerden, blijft de Pythagoreïsche Stelling een tijdloos symbool van de schoonheid en universaliteit van de wiskunde.